Auteur: Bernard Nelleke
In deel 1 is het artikel gestopt met de zin: Maar Guido van Arezzo heeft meer belangrijke dingen gedaan op muziekgebied. Hij wordt dan ook gezien als een van de belangrijkste grondleggers van de muzieknotatie. We gaan nu verder…
Hij werd geboren in 991 in Arezzo en hij stierf in 1033 in Avellano. Hij studeerde in de benedictijnenabdij van Pomposa, bij Ferrara. Daar ervoer hij de moeilijkheden die zangers hadden met het onthouden van toonhoogten in de Gregoriaanse gezangen. Hij ging zoeken naar vereenvoudiging. Het resultaat werd een eigen notatiesysteem (balk en noten), dat het mogelijk maakte de gezangen veel sneller te leren. Ja zelfs ze direct van blad te zingen.
Nu moeten we weten dat de muziek in zijn tijd gebruik maakte van verschillende diatonische toonladders. Men spreekt van diatonische toonladders wanneer deze bestaan uit twee soorten troonsafstanden (dia = dubbel). Die twee soorten zijn de halve en de hele toonafstand. In muziektermen de kleine en de grote secunde.
Men kende in die tijd dus meerdere soorten diatonische toonladders. De zogenaamde modi (enkelv. modus). En bij elke modus lagen de kleine en de grote secunde op steeds andere plaatsen. Dat maakte de zaak er niet bepaald eenvoudig op, want hoewel men al vóór de tijd van Guido de nootnamen a-b-c-d-e-f-g kende, was het niet duidelijk waar zich die halve toonafstand bevindt.
Guido nam nu de Johannes-hymne van Paulus Diaconus en maakte er een melodie bij, zodanig, dat elke regel één toon hoger begint. De tekst van de hymne is:
Ut queant laxis
resonare fibris
mira gestorum
famuli tuorum
solve polluti
labii reatum
Sancte Iohannes!
met noten als volgt:

En in modern notenschrift aldus:

Hieronder ziet u nogmaals de ontwikkeling.
Links de Latijnse namen, daarnaast de neumen, dan de kwadraatnotatie en rechts de moderne schrijfwijze van de toonhoogte.
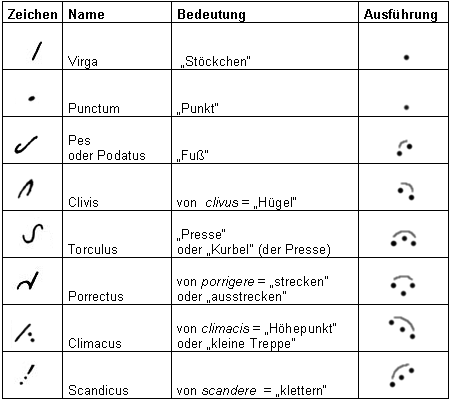
Terug naar de Johannes-hymne
In de hymne begint iedere regel één toon, één secunde hoger. Guido gebruikte de beginlettergrepen van elke regel van het gedicht ut-re-mi-fa-sol-la als basis van zijn vastlegging. Het is een reeks van 6 tonen. Een dergelijke reeks noemt men een hexachord. (Het woord stamt uit het oud-Grieks en betekent zes snaren).
Met de door Guido gegeven benaming zag dat hexachord er aldus uit: ut – re – mi – fa – sol – la, overeenkomend met c – d – e – f – g – a. De halve toonafstand bevindt zich precies in het midden: mi – fa. (e – f). De overige toonafstanden zijn hele-toons toonafstanden. Door dat midden heeft de zanger nu houvast gekregen. (In de bestaande toonladders, die bovendien bestaan uit 7 tonen, ofwel 6 toonafstanden verdeeld over 4 hele en 2 halve afstanden, is van een midden geen sprake. Dus geen houvast.)
Problemen deden zich evenwel voor bij het instuderen van melodieën, waarvan de omvang groter is dan de omvang van een hexachord. Dan waren de zes lettergrepen niet voldoende. Daar kwam ook nog bij dat in sommige melodieën een verlaagde toon b, (dus bes), voorkwam. Maar in het systeem, zoals hierboven, kwam er alleen maar een halve toonafstand voor tussen de tonen mi en fa (e en f).
Guido breidde dan ook het hexachord uit met een hexachord eronder en een hexachord erboven die elkaar gedeeltelijk overlappen en hij benoemde ze als volgt:
f - g - a - b - c - d - e - f - g - a - b - c - d - e - f - g
ut - re - mi - fa - sol - la (hexachordum mollum = zacht)
ut - re - mi - fa - sol - la (hexachordum naturale)
ut - re - mi - fa - sol - la (hexacghordum durum)
Guido ontwikkelde daarna een compleet toonsysteem gebaseerd op deze hexachorden. In feite was het gebaseerd op het verplaatsen van de hexachorden.
Hij constateerde wel dat in het onderste hexachord iets wrong. De afstanden mi – fa – sol = ½ + 1 kwam niet overeen met a – b – c = 1 + ½.. Er bleken dus twee soorten b te bestaan. Daarom ging hij in het hexachordum mollum uit van een verlaagde b en noteerde die als een ronde b. Dit zou later het verlagende molteken worden: b wordt verlaagd tot bes.
De andere b in de beide hogere hexachorden kregen ter onderscheiding van de lagere b een vierkante b genoteerd. Hieruit ontstond later het herstellingsteken.
En tot op de dag van vandaag heet in Duitsland de Bes = B en de B = H. Dat verklaart waarom in Duitsland zo vaak in de muziek het motief Bes A C B voorkomt. Is in het Duits: B A C H.
Door dit alles was het nu beter mogelijk geworden van blad te zingen.
Guido ondersteunde de zangers door met de linkerhand aan te geven welke toon getroffen moet worden. De onderdelen van de hand, zoals de vingerkootjes had hij, met de nootnamen aangeduid, zoals hieronder weergegeven.
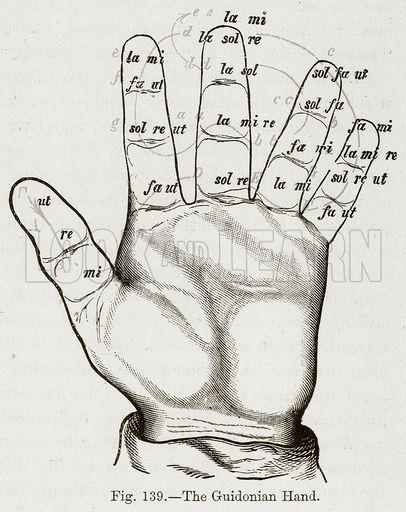
Dit systeem van handzingen werd in onze tijd, zij het met enige wijzigingen, opnieuw ingevoerd door de Amsterdammer Willem Gehrels, en heeft alom erkenning gevonden in het muziekonderwijs.
Later heeft men de reeks aangepast door de ut te vervangen door do wat tot een betere zingbaarheid leidde. Ook heeft men later een 7e toon in de reeks opgenomen door de beginletters van Sancte Ioannes samen te voegen tot de toon si. Aldus ontstond de overbekende reeks do – re – mi – fa – sol – la - si – do.
Een aantal jaren geleden heeft men geprobeerd de sol vervangen door so om aldus een consequente vorm van twee letters te maken. Ook heeft men geprobeerd de si te vervangen door ti, waardoor alle beginletters verschillend werden, maar deze laatste twee veranderingen hebben nooit algemeen ingang gevonden.
Overigens is het vandaag de dag zo dat in de noordelijke helft van Europa de nootnamen benoemd worden met de letters van het alfabet: c – d – e enz. In de zuidelijke helft met de namen van do – re – mi enz. Ook dit is cultureel erfgoed.
Nu restte er nog één groot probleem, namelijk “Hoe lang duurt een toon ten opzichte van een andere toon?”
Men kende wel de volgende rangschikking:
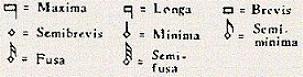
In de 14e eeuw is in Zuid-Frankrijk en Noord-Italië een stroming ontstaan die zich Ars Nova noemt. Ars Nova betekent nieuwe techniek. Dit als tegenstelling tot de oude componeerkunst. Men beschouwde deze laatste als hopeloos verouderd en noemde die oude stijl dan ook Ars Antiqua ofwel oude techniek.
Die Ars Nova brengt nog al wat vernieuwingen aan in de muziek. Die vernieuwingen hebben onder meer betrekking op de muzieknotatie, speciaal de notatie van het metrum. Tot dan toe was het metrum, en dus ook de onderverdeling van de noten in het notenschrift, driedelig. Dit onder invloed van de drievuldigheidsleer. Dat kwam er op neer dat een bepaalde nootwaarde altijd drie keer groter was dan zijn daarop volgende kortere. Of omgekeerd, dat de eerstvolgende grotere nootwaarde altijd drie keer langer was. Een driedeligheid dus.
In de Ars Nova nu vindt ook de twee-deligheid, de onderverdeling van noten in tweeën, erkenning. Maar daarvoor was het wel nodig dat in het muziekschrift werd aangegeven wanneer een onderverdeling in twee of in drie gewenst was.
De driedelige onderverdeling noemde met de volmaakte manier, de modus perfectum. De tweedelige manier de onvolmaakte, ofwel modus imperfectum. Populair gezegd: er ontstond nu naast de driedelige maatsoort ook een tweedelige maatsoort.
Die twee-deligheid was overigens al lang gemeengoed in de wereldlijke muziek en in de volksmuziek. Lopen, weven, spinnen, dorsen, dansen, enz. zijn immers tweeledige handelingen waarbij gezongen werd. Nu werd vrijwel al deze muziek niet opgeschreven, maar gewoon mondeling doorgegeven van vader op zoon, van moeder op dochter, enz.
Maar de ‘officiële’ muziek gaat zich nu ook interesseren voor de wereldlijke muziek. Ja zelfs elementen uit de volksmuziek in zich opnemen.
Voor de liturgische muziek zal het nog ruim een eeuw duren vooraleer de twee-deligheid daar ingang vindt.
Die Ars nova beweging wordt gezien als een van de keerpunten in de geschiedenis van de notatie. En dan vooral voor de precisering daarin. Naast de bestaande driedelige metriek (driedelig vanwege de Goddelijke drie-eenheid) komt er een twee-deligheid. M.a.w. naast de al bestaande 3-delige maat komt er nu ook een 2-delige, maar daarnaast ook tussenvormen. Men kan nu de duur van de noten onderling afmeten. Men spreekt dan van de mensurale (ofwel gemeten) notatie. Dit mensurale systeem ziet er als volgt uit:
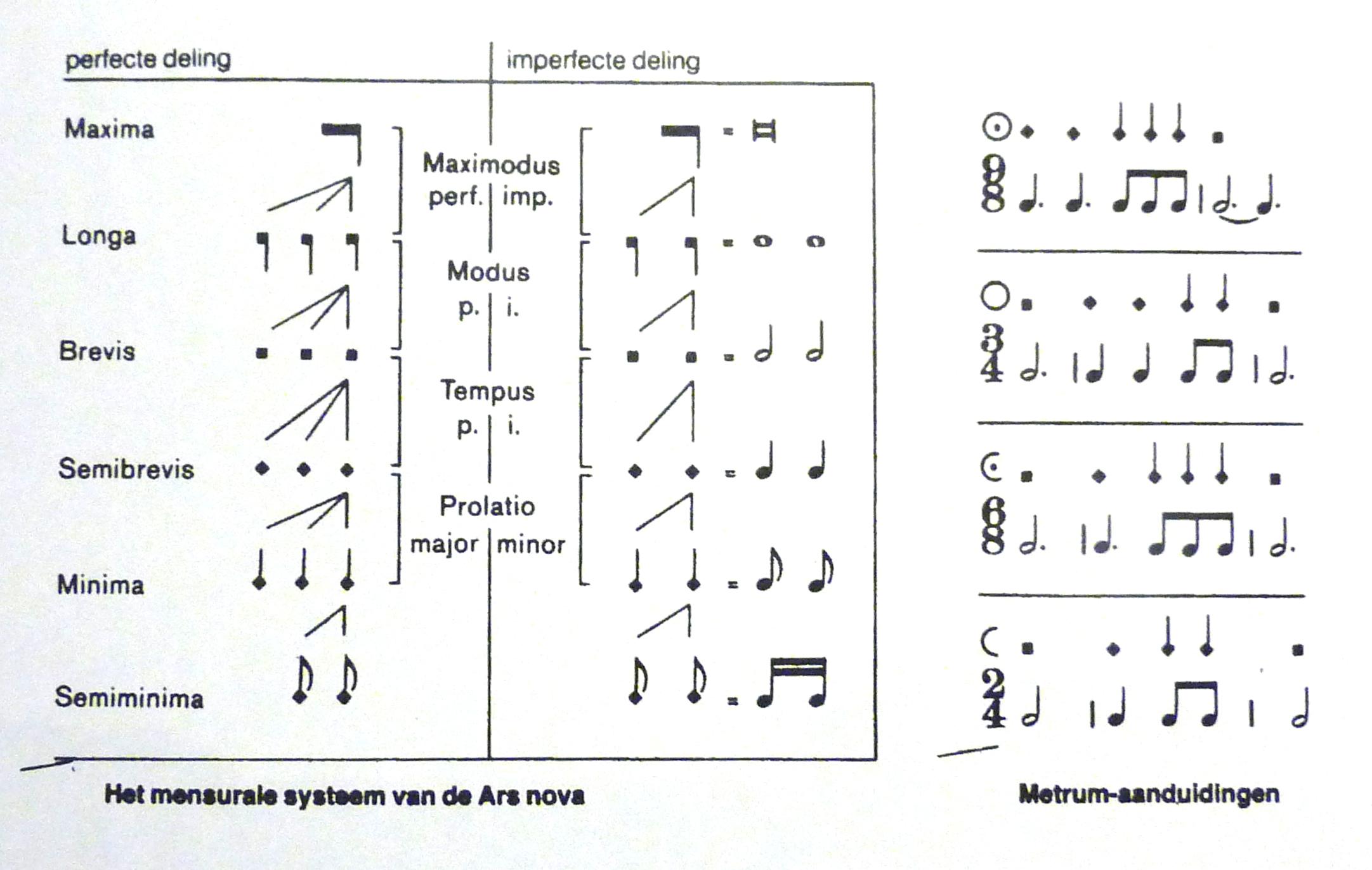
Aan het eind van de regel staat de moderne noot weergegeven.
Maar wil dit systeem effectief zijn, dan is het wel noodzakelijk aan te geven wanneer er van drie- of van twee-deligheid sprake is. Dat deed men aldus: de onderverdeling in drieën noemde men de modus perfectum (de volmaakte manier). Dit gaf men aan door middel van de meest volmaakte wiskundige figuur voor aan de balk. En dat was de cirkel.
De onderverdeling in tweeën noemde men, zoals gezegd, de modus imperfectum (de onvolmaakte manier) en gaf men aan d.m.v. de meest onvolmaakte wiskundige figuur, ofwel de halve cirkel. Die halve cirkel ligt nog altijd ten grondslag aan ons teken voor een vierkwartsmaat.
Door dit systeem, waarin in feite de twee-deligheid gelijkgesteld werd met de drie-deligheid, werd de wereldlijke muziek, muzikaal gezien, evenwaardig aan de geestelijke muziek..
Later zijn de hoekige notenfiguren vervangen door ronde figuren. En daarmee was ons muzieknotatiesysteem geworden wat het nu is.
Zie ook http://nl.wikipedia.org/wiki/Geschiedenis_van_de_muzieknotatie
